量子暗号通信 ~絶対に解読されない暗号通信~
メルマガ読者のBekohさんが、将来のセキュアな通信技術の「量子暗号通信」
について、概要をまとめてくださいました。2回にわたって、その記事を掲載
させていただきます。
目次
(7)量子コンピュータの概念の誕生から現在の研究
(8)量子暗号の必要性
(9)現在の量子暗号通信の進歩
(10)量子暗号通信の考え方
(11)不確定性原理の議論
(12)終わりに
(7)量子コンピュータの概念の誕生から現在の研究
今回は量子コンピュータがメインではないので簡単にしか説明しませんが、最
初に理論的に考案したのは1985年イギリスの物理学者デイビット・ドイチュで
す。結論から言うとドイチュの考えている量子コンピュータは必ずしも正しい
とは言えませんが、量子コンピュータの基礎を築いたのは確かです。
(8)量子暗号の必要性
まだまだ発展途上ですが量子コンピュータが実現すれば今の暗号通信はほとん
ど意味を成さなくなってしまいます。例えば、1万桁の整数を因数分解するに
は、現在のスーパーコンピュータでは1000億年以上もの時間がかかりますが量
子コンピュータならたったの数時間で終えられると言われています。現在イン
ターネットなどで普及している「RSA暗号」は、因数分解の困難さをもとにつ
くられている為、将来量子コンピュータが実現したら、RSA暗号で暗号化され
た文章は簡単に解読されてしまいます。そうなると、現在の暗号通信は子供だ
ましのようなもになってしまいます。これだけがすべての理由ではもちろんあ
りませんが、「量子暗号通信」はいくら時間をかけても「絶対的に」安全であ
る為、非常に重要なのです。例えば、国家間の機密情報のやり取りなどを考え
た場合、絶対に安全である通信が求められる為、必要性は十分高いのです。何
億年というとてつもない時間をかけても解読されないのですから。
(9)現在の量子暗号通信の進歩
そして実験室レベルですが、量子暗号通信の実用化の第一歩を1989年に踏んで
います。
国内では2000年9月14日に成功しています。
http://www.mitsubishielectric.co.jp/news/2000/0914.htm
そして、2002年、世界最長となる87kmの量子暗号通信システムに成功していま
す。
http://www.mitsubishielectric.co.jp/news/2002/1114.htm
そして更に2005年に、国内初量子暗号システムの相互接続実験に成功していま
す。
http://www.mitsubishielectric.co.jp/news/2006/0512.htm
これは、民間の企業が主導権を握って行われました。その組織は、三菱電機と
日本電気で、客観的な検証を東京大学生産技術研究所が行っています。民間の
2社が開発して、大学が検証したというものです。
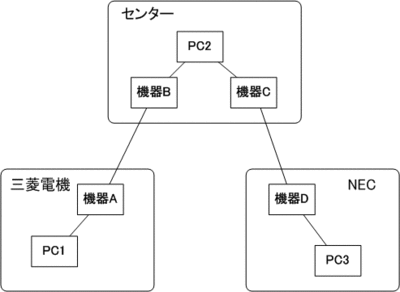
実験概要を示します。
図に、三菱電機製量子暗号システムとNEC製量子暗号システムを相互接続した
量子暗号ネットワークの構成を示します。従来、三菱電機製の量子信号システ
ム(機器A-機器B)とNEC製の量子暗号システム(機器C-機器D)は、それぞれ独立
に構成され、各がくのシステム内に閉じた通信が行われていました。異なる量
子暗号システムをネットワーク化するためには、それらを中継する手順と方式
が必要です。今回、それぞれのシステムに影響を与えることなく、相互接続可
能な中継方式を新たに開発し、量子暗号ネットワークの構築に成功しました。
ネットワークとしての安全性は東大生研で理論的に解析しました。
構築した量子暗号ネットワークで、鍵を共有する手順は次のとおりです。
まず、機器A-機器B間と機器C-機器D間、それぞれの通信に適用する鍵を、量子
暗号を用いて設定します。機器A-機器Bの間では鍵K1を共有、機器C-機器Dの間
では鍵K2を共有します。
次に機器A-機器Dが最終的に共有すべき鍵K3をセンターで生成し、機器Bと機器C
を通じて機器Aと機器Dに送ります。機器Bから機器Aには鍵K1を用いて暗号化し
た鍵K3を送り、機器Cから機器Dには鍵K2を用いて暗号化したK3を送ります。機
器Aと機器Dは量子暗号の理論に基づく安全な方法で鍵K3を共有できたことにな
ります。このK3を暗号鍵として機器Aと機器Dはデータのやりとりを安全に行う
ことが可能となります。
ちょっと実験内容の原理が分かりづらいですが、要は異なる量子暗号通信機器
で相互接続できたということです。そのうち、OSI参照モデルのような標準モ
デルがゆくゆくはできるかもしれませんね。まぁ、その前に各種ベンダーで競
い合ってもらった方ほうが「量子暗号通信」の普及は進むと思いますが。
(10)量子暗号通信の考え方
まず、基本原理は量子力学の「不確定性原理」という原理を利用しています。
簡単にどのような原理かというと、「同時に速度と位置は観測できない」とい
うものです。これはニュートンが発明した力学と決定的に違います。今や古典
力学とも呼ばれるニュートンの力学は「同時に速度と位置は観測できます」。
ミクロの世界(電子や原子核のスケール)では、普段私たちが日常生活を営んで
いる物理法則が成り立たないのです。しかし、ご存知の通り、コンピュータは
電気信号(電子のスケール)で通信を成り立たせているのですから、うまく使え
ば量子力学の原理を応用することができるのです。この逆手をとったような方
法で絶対に解読されない暗号方式が考えられたのです。
しかし、暗号通信は今までの経験から、どこかでほころびがでてきて、ハッカ
ーや悪意ある第三者に破られるのではないかと懸念する情報処理技術者もいま
す。実際、この話を同僚にすると、その完全な安全性に疑問を抱いていました。
そこで簡単な原理を考えながら何故この暗号通信が「絶対完全」に安全なのか
ということを考えましょう。それには難しい量子力学の知識が無くても「不確
定性原理」の意味を良く理解すれば「完璧な安全性」の理由が解ります(多分)。
まず観測可能な「位置」と「速度」を○と♂で図式化します。
位置:○
速度:♂
最初に古典力学で考えましょう。「位置」と「速度」は「同時に」観測可能です。
位置確定 速度確定 「○」 「♂」
ところが量子力学では「位置」と「速度」が同時に観測不可能です。位置を確
定しようとすると速度が正確に観測不可能になります。
位置確定 速度不確定 ↑ 「○」 ←♂→ ↓
その逆もしかりで速度を確定しようとすると正確な位置が観測不可能になりま
す。
位置不確定 速度確定 ↑ ←○→ 「♂」 ↓
どちらか一方を確定(観測)するともう一方が不確定となり、その変化によって
盗聴されたことが検出されるという仕組みです。
(11)不確定性原理の議論
量子論の重要な性質である「不確定性原理」は、1927年にハイゼンベルグによ
って発見されたものです。これは、単純な理論ですが古典力学とは全く相容れ
ない原理です。今でこそ高校生の教科書に載るくらい有名な原理ですが当時と
しては画期的な考え方でした。その証拠に物理学の巨人、アインシュタインは
終生この原理に納得していませんでした。有名な「神はサイコロを振らない」
という隠喩で批判しています。量子力学自体に反対していたのです。それにし
てもアインシュタインの業績の中には量子論に関わるものも多くあり皮肉的と
も思えます。
(12)終わりに
私が以前から思っていたことなのですが現在のIT化の時代は1900年頃に産声を
上げた量子力学のノリと似ているなぁと思います。どちらも日常生活を一変さ
せる技術ではないかと思います。ただ幸運なことに量子力学が極限られた天才
によって発展してきたのに対して、情報通信技術社会の現代は低予算で誰でも
この激変の舞台に参加することができるということです。しかも仕事にすれば
お金にもなり安定した生活を送ることが出来ます。これはすばらしいことだと
思いませんか?
さまざまな技術の進歩には本当に目を見張るものがあります。今後10年後には
この量子暗号通信の技術も本格的に実用化されるのではないかと思います。そ
うすると各種の情報処理試験の問題にもこの分野の問題が当たり前のように出
題されるかもしれませんね。量子通信暗号だけでなくこの原理を利用した量子
コンピュータ(量子計算機)の研究開発もさかんに進められていることは簡単に
触れました。今後、情報処理技術の世界が一変するような感じもします。今回
は「量子暗号通信」に的を絞って簡単に解説しましたが、「量子コンピュータ
(量子計算機)」の分野もこれから勉強していきたいですね。実用化にはまだま
だ幾多の困難が予想されますが近い将来きっと実用化されるでしょう。実際に、
現在の大学の理工学部の一部の学科の授業ではこの分野の講義がすでに行われ
ています。
最後に、私はこの分野の研究者でもなければ開発者でも関係者でもありません。
ただ大学時代に量子力学を専攻していて、その物理学の原理が情報処理技術の
世界に応用されていることを知って、興奮しているだけなのです。なので、第
三者の私がこんな記事を書くことに躊躇もしました。ただ興味はすごくあって
自分なりにまとめたくて、今回拙い記事として書かせていただきました。この
未開の分野の研究者や開発者に敬意を表します。
参考Webサイト
http://www.mitsubishielectric.co.jp/pr/index.html
参考図書
・Newton 2006年7月号(株式会社 ニュートンプレス)
・Newton 別冊 みるみる理解できる量子論(株式会社 ニュートンプレス)
・図解 量子論がみるみるわかる本(PHP研究所)